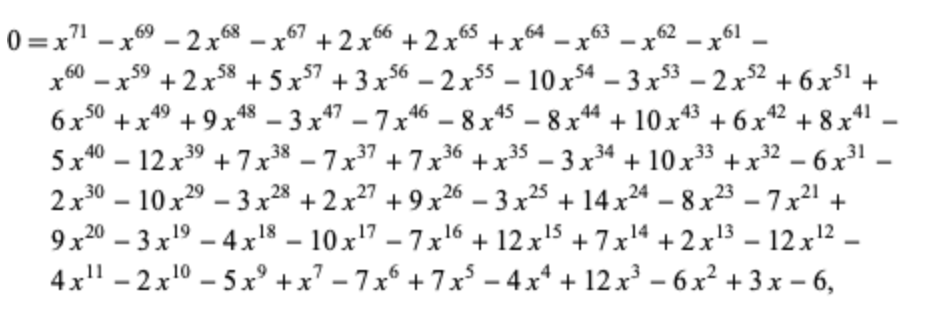دنباله‌ی ببین و بگو (look and say)

ببین و بگو!

1

در سطر بالا چه می‌بینید؟ جواب:

ی دونه یک (یکی یک)

11

حالا در سطر بالا چی می‌بینید؟ جواب:

دو تا یک

21

حالا مجددا، در سطر بالا چی می‌بینید:

ی دونه دو، و ی دونه یک

1211

الگویی که جمله بعدی رو بدست می‌آوریم، ساده است؛ 

ببین و بگو

در عدد بالا،1211 چی می‌بینید، از سمت چپ که بخونیم:

ی دونه 1 (11)

ی دونه 2 (12)

دو تا 1  (21)

پس جمله بعدی دنباله می‌شود:

111221

و به همین ترتیب، بقیه جملات بدست می‌آید:

312211

13112221

1113213211

...

دنباله بالا چند ویژگی دارد که بعضی از آن‌ها جالب و اثباتشون سخت هست:

• 1. دنباله و الگوی بالا بازگشتی هست، یعنی جمله فعلی رو می‌توان توسط جمله (جملات) قبلی بدست آورد.
• 2. فقط رقم‌های 1و2و3و در جملات بالا ظاهر می‌شود. یعنی اگر بقیه جملات الگو را بنویسیم، رقم‌های 6و5و4و... هرگز ظاهر نمی‌شود.( اثبات کمی سخت، ولی در حد دانش‌آموز دبیرستانی هست، به  کمک برهان خلف)
• 3. طول دنباله (تعداد رقم‌های آن) افزایش پیدا می‌کند.(واضح هست). ولی اگر چند جمله‌ی دیگر دنباله را بنویسیم. یک الگو در مورد رشد طول دنباله پیدا می‌شود.

جان کانوی، ریاضیدان معروف انگلیسی، ثابت کرده است که این رشد طول، به صورت یک تصاعد هندسی با قدر نسب r=1.30357726...9...0 هست. که این عدد خودش گنگ و ریشه‌ی مثبت و حقیقی چندجمله‌ای درجه‌ی 71،! زیر هست:

مکان تنها ریشه‌ی مثبت حقیقی معادله بالا را، در شکل زیر می‌بینید:

کانوی در واقع ثابت کرد که بلوک‌های تشکیل دهنده هر جمله دنباله بعد ار مدتی ثابت و یکسان می‌شوند.

جمله اول دنباله بالا با یک شروع شد، در واقع فرقی نمی‌کند با 1 یا 2 یا 3و... شروع شود. دنباله دوباره، تناوبی می‌شود.

حال به عنوان تمرین دنباله را از 2 شروع کنید و ببینید و بگویید:

2, 12, 1112, 3112, 132112, 1113122112, 311311222112, ...

منبع:

1.http://mathworld.wolfram.com/topics/NumberTheory.html

2. کتاب ریاضی تکمیلی هفتم